India’s F&O trading has seen record-breaking volumes, but most retail traders have faced heavy losses raising many red flags for SEBI. To address this, SEBI has now introduced several changes to this segment that could reduce this segment’s trading volume by approximately 30%, returning them to 2022 levels. While this will reduce the retail traders’ presence they will still prevail. Hence, understanding the nuances of options trading is now more crucial than ever. One key aspect often overlooked is the Options Greeks Rho. Want to learn how it impacts your trades? Check out this blog for a quick dive into this vital concept!
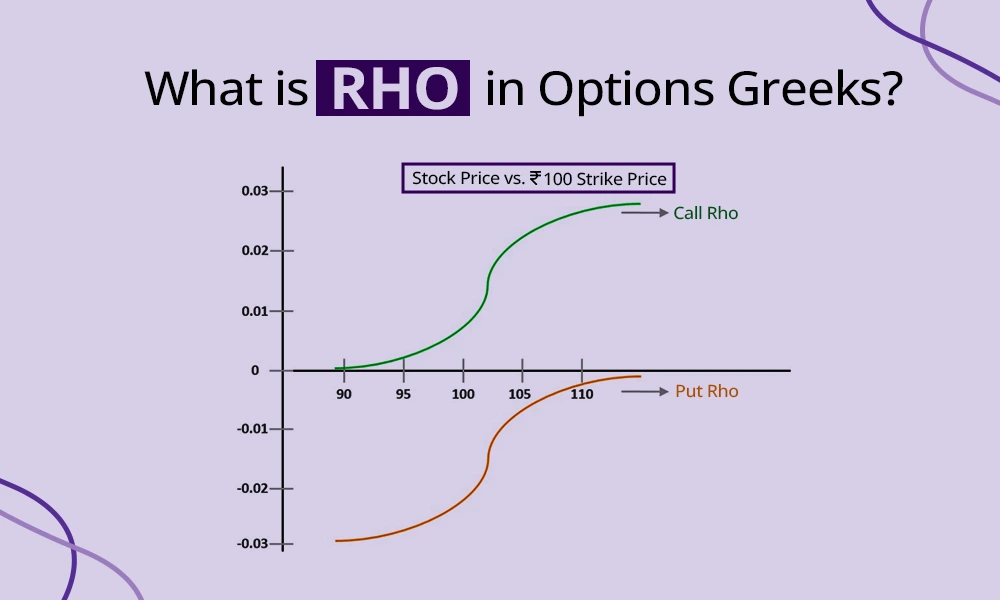
Rho is one of the final stages of options greeks and may be less used as compared to its counterparts like Delta, Gamma or Theta. While Delta and Gamma measure the changes in the price of the underlying asset and its impact on the options, Rho measures the sensitivity of an option's price to changes in the risk-free interest rate. It essentially tells how much the price of an option (its premium) is expected to change for every 1% change in the interest rate.
Rho is more significant for longer-term options as interest rates have a greater impact on the value of cash flows over extended periods. Rho is usually positive for call options as higher interest rates increase the present value of owning the underlying asset. Conversely, Rho is negative for put options since higher rates make it less appealing to defer selling the underlying asset.
Rho is especially important for traders in a country like India where interest rates can fluctuate due to RBI policies as well as Fed rates. Rho can be particularly helpful in certain market conditions, especially for institutional traders or strategies involving long-dated options. However, for short-term traders, Rho often has a minimal impact when compared to other Greeks like Delta or Vega.
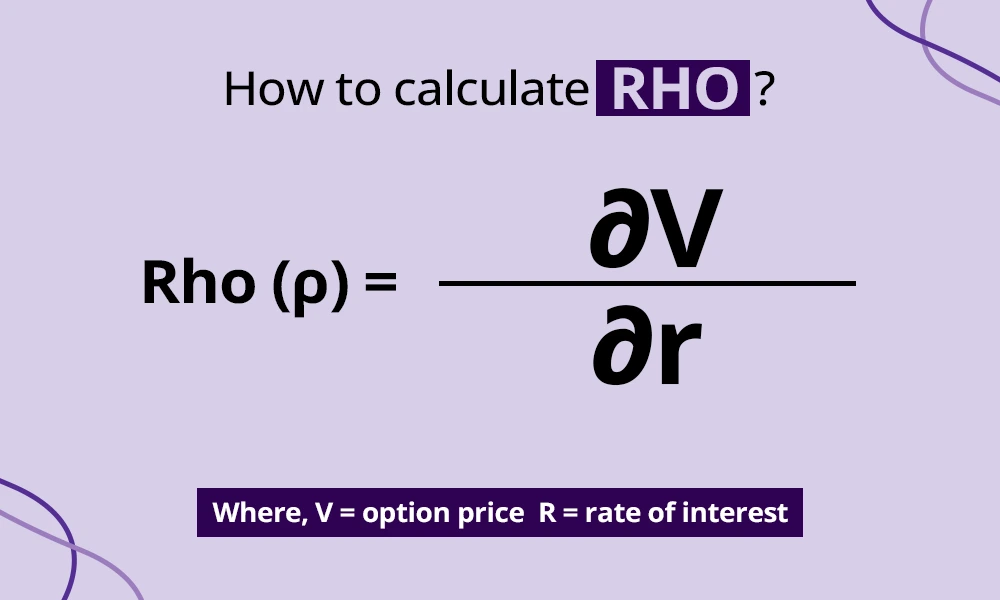
The calculation of Rho can be quite complex and uses a formula derived from the Black-Scholes model for European-style options. However, let us consider a very basic and simple formula for the calculation of Rho.
The formula to calculate Rho is,
Rho (ρ) = ∂V / ∂r
Where,
V = option price
R = rate of interest
The above formula for Rho is quite basic but can explain the impact of interest rate fluctuations on options pricing, enabling traders to make informed trading decisions. Let us now understand the calculation of Rho using a simple example.
Consider a trader with a call option on a stock with the current price of the call option of Rs. 10 and a risk-free interest rate of 5%. If the risk-free interest rate increases to 6%, and the price of the call option increases to Rs. 10.50, the Rho for the option will be calculated as below.
Initial Option Price (V0) - Rs. 10
Final Option Price (V1): Rs. 10.50
Initial Risk-Free Rate (r0): 5% or 0.05
Final Risk-Free Rate (r1): 6% or 0.06
Using the Formula for the calculation of Rho
Rho (ρ) = ∂V / ∂r
Rho (ρ) = (V0 - V1) / (r0 - r1)
Rho (ρ) = (10.50-10) / (0.06 - 0.05)
Rho (ρ) = 0.50 / 0.01 = 50
Therefore, the Rho of the above example is 50.
This shows that for every 1% increase in the risk-free interest rate, the price of the option will increase by Rs. 50.
Now that we have seen the calculation of Rho, let us now move on to the interpretation of Rho for different types of options.
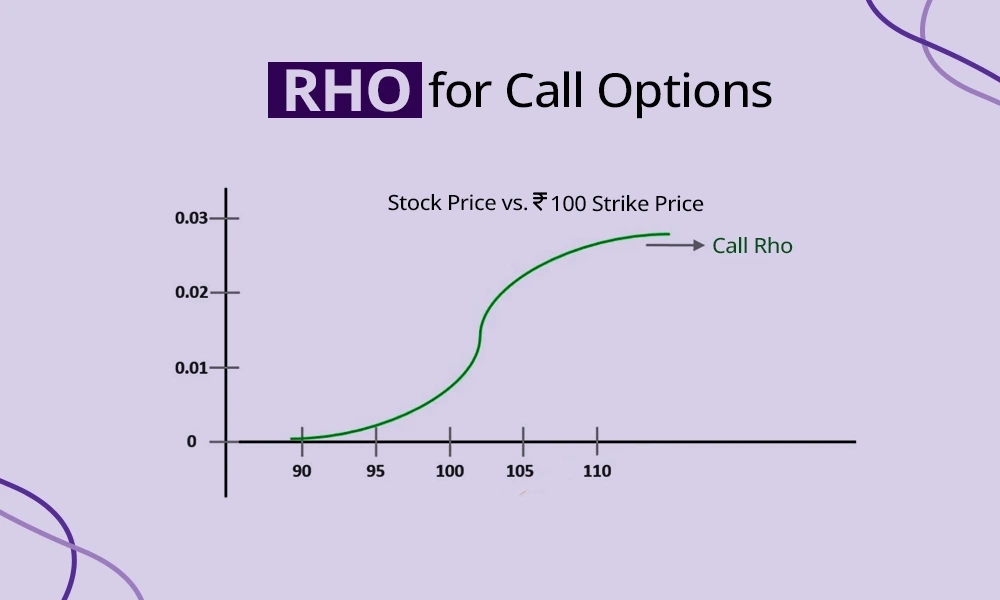
Rho is positive for call options which means that the value of the call options increases when the risk-free interest rate rises. This occurs because higher interest rates reduce the present value of the strike price (the amount the trader would pay to exercise the option in the future). A lower present value of the strike price makes the option more attractive, increasing its price. Thus, if a trader is holding a long position on a call option of Nifty, a rise in the interest rate can increase the value of their position. This is particularly important when trading options on high-value assets where interest rate changes can have a noticeable impact. However, this effect is usually subtle compared to factors like implied volatility and time decay.
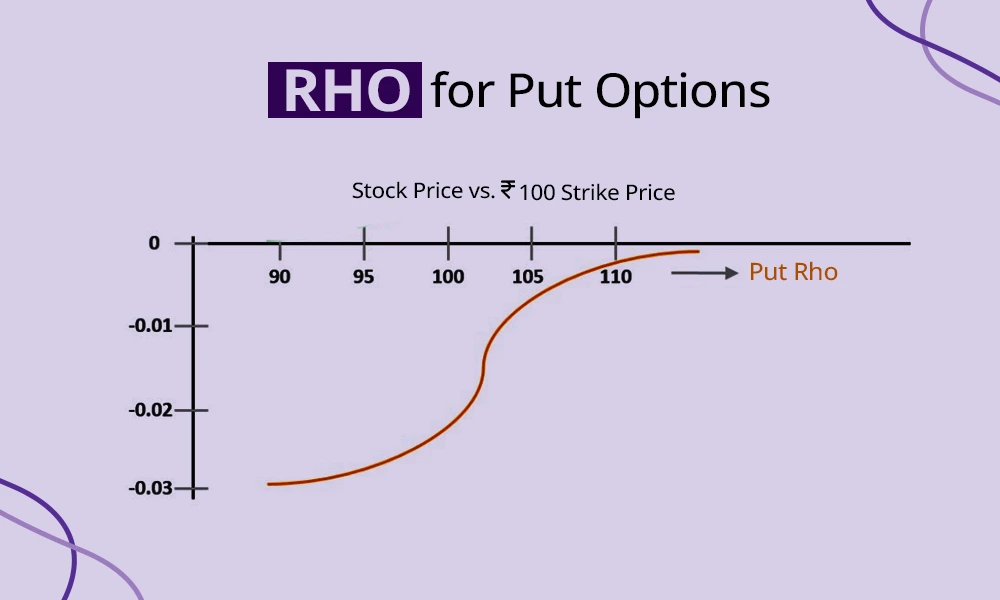
Rho is negative for put options and indicates that an increase in the interest rates will decrease the value of a put option. This happens because higher interest rates make it less attractive to hold money to buy a put option. Moreover, the present value of the strike price reduces, which negatively impacts the payoff of the put option, lowering its value. Thus if a trader is holding a long potion on a put option on a stock or index, an increase in the rate of interest will erode the value of the option. Similarly, if the interest rate is expected to decrease, the value of the put option may increase slightly.
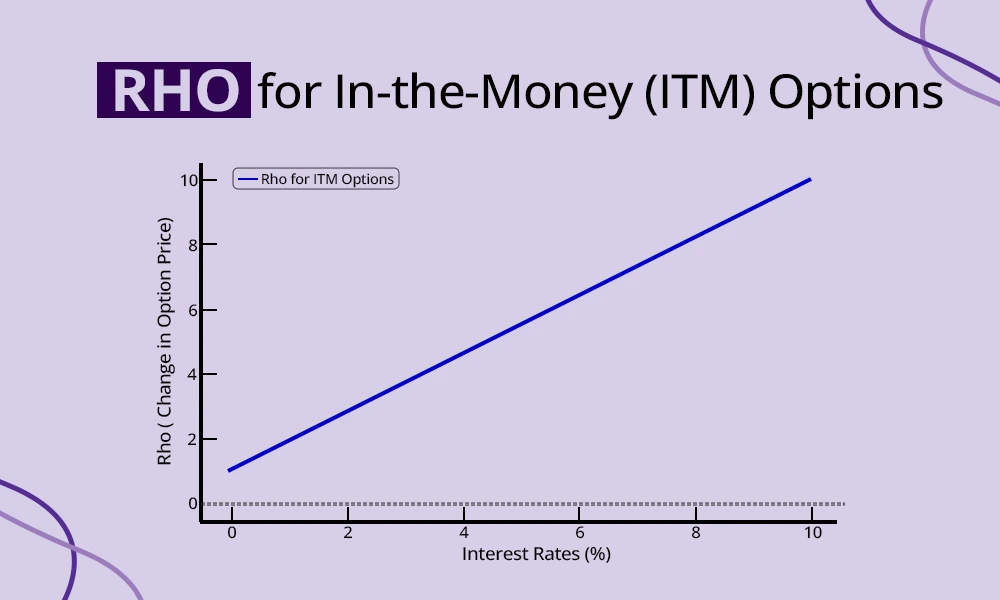
In-the-money options (both calls and puts) have a more pronounced Rho because they already have intrinsic value. Since these options are closer to or already profitable to exercise, changes in the risk-free interest rate significantly impact their valuation. For example, an ITM call option on Reliance Industries could see a substantial price increase if interest rates rise, while an ITM put option may lose value. Traders who trade ITM options should, therefore, pay close attention to Rho, especially during periods of interest rate volatility due to its potential to amplify the overall profit or loss.
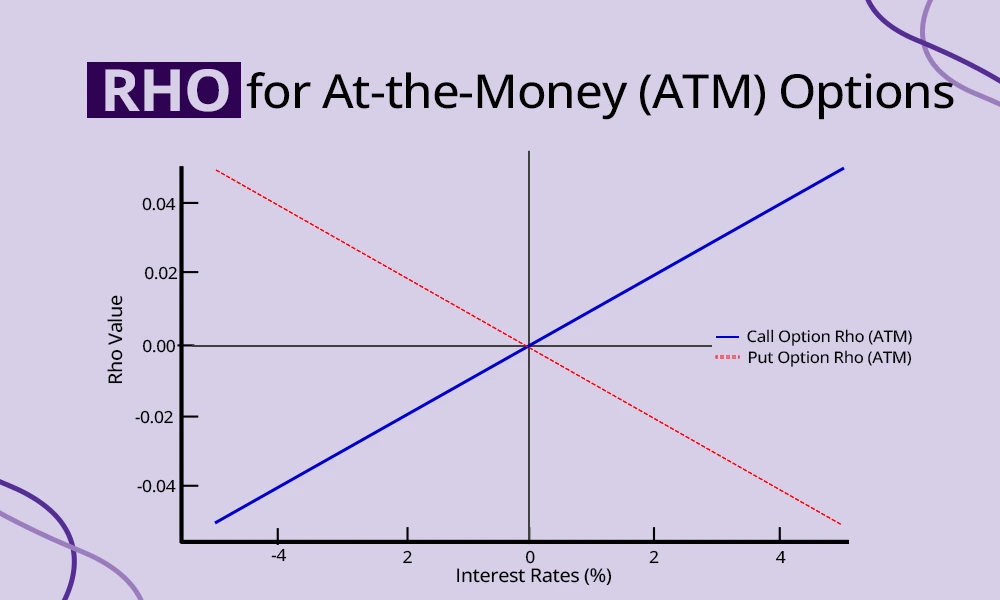
At-the-money options are those where the strike price is close to the current market price of the underlying asset. These options tend to have a moderate Rho compared to ITM and OTM options. While the impact of interest rate changes is not as significant as for ITM options, it is still noticeable because ATM options are highly sensitive to changes in option pricing factors like time value and volatility. For example, an ATM call option on the Nifty 50 or an individual stock like HDFC Bank will increase in value slightly if interest rates rise, whereas an ATM put option will decrease in value. Since ATM options are widely used for directional trading or hedging, understanding their Rho can help traders adjust their positions to align with expected interest rate movements. This is especially useful in short-term trading strategies where ATM options are commonly employed.
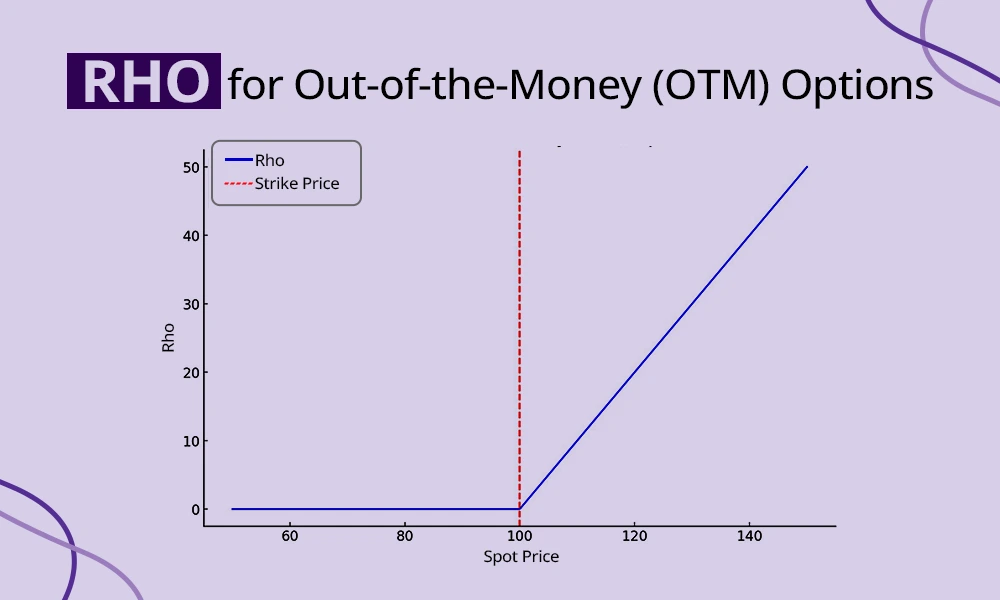
Out-of-the-money options (both calls and puts) are less sensitive to changes in interest rates and thus have a lower Rho. This is due to the OTM options derive their value primarily from time and volatility rather than intrinsic value. For example, an OTM call or put option on, stocks like Tata Motors will likely show minimal price movement due to interest rate changes. However, traders holding large positions or using options in a hedging strategy should still consider Rho, as even small changes can add up over time.
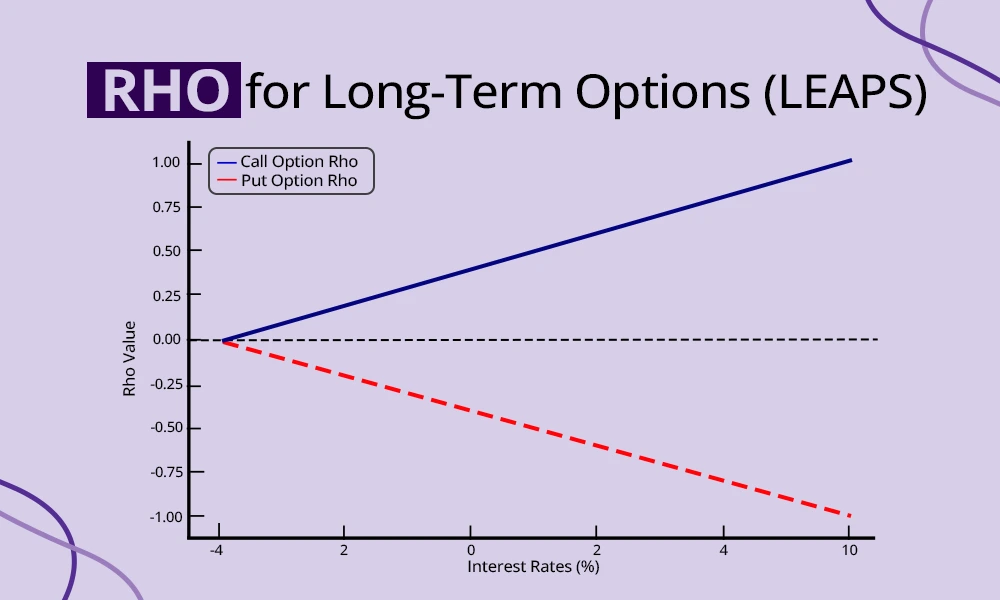
Long-term Equity Anticipation Securities (LEAPS) are options with expiration dates typically a year or more in the future. As Rho’s impact on the options increases with the time to expiration, it becomes quite relevant for LEAPS. An increase in the rate of interest for call LEAPS increases their value making them more appealing, while put LEAPS lose value in such cases. Therefore, traders trading in LEAPS for indices or stocks can use Rho to anticipate how RBI rate announcements might affect their positions.
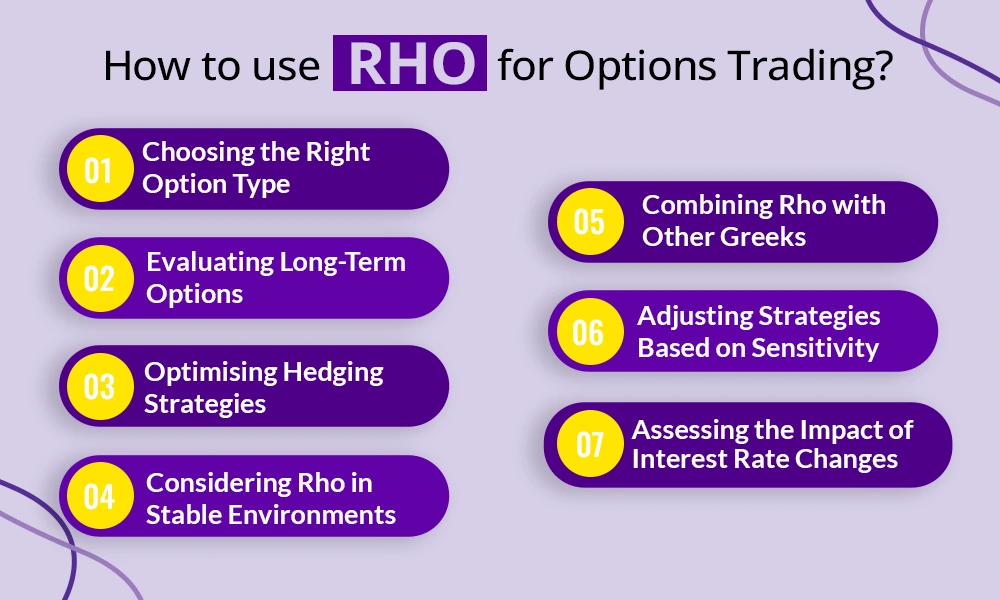
The interpretation of Rho for different option types allows traders to devise a suitable trading strategy and have profitable outcomes. The use of Rho in a trading plan can be explained hereunder.
Assessing the Impact of Interest Rate Changes
Rho allows traders to estimate how much an option's price will change if the Reserve Bank of India (RBI) adjusts interest rates. For instance, a rise in interest rates typically benefits call options and negatively impacts put options.
Choosing the Right Option Type
Traders can consider buying call options or selling put options if they anticipate an increase in interest rates. Conversely, put options may become more favourable if interest rates are expected to decrease.
Evaluating Long-Term Options
Since Rho has a more significant impact on long-term options, such as LEAPS, traders can use Rho to account for the cumulative effect of interest rate changes over time when dealing with these options.
Optimising Hedging Strategies
Rho can assist traders in selecting options that minimise the impact of interest rate fluctuations on their overall hedging strategies.
Considering Rho in Stable Environments
Even in low-volatility or stable interest rate conditions, Rho remains relevant during periods of economic uncertainty or when central banks actively adjust rates.
Combining Rho with Other Greeks
Traders can integrate Rho with other Greeks, such as Delta, Gamma, and Theta, to gain a comprehensive understanding of the various factors influencing their options trading strategies.
Adjusting Strategies Based on Sensitivity
Recognising that in-the-money (ITM) and long-term options are more sensitive to Rho than out-of-the-money (OTM) and short-term options enables traders to adjust their strategies to manage risk effectively.
Rho is an essential Greek that helps traders understand the sensitivity of options prices to changes in interest rates, making it particularly relevant during periods of fluctuating monetary policy. While this may be a less known or used options greeks, integrating it with other greeks and assessing its impact on different types of options can help traders implement better trading or hedging strategies thereby ensuring profitability for the portfolio as a whole.
This is the final greek in our series of option greeks and yet another attempt to simplify options trading and its related concepts. Let us know your thoughts on this topic or if you need further information on the same.
Till then Happy Reading!
Read More: Open Interest in the Stock Market
Marisha Bhatt is a financial content writer @TrueData.
She writes with the sole aim of simplifying complex financial concepts and jargon while attempting to clarify technical and fundamental analysis concepts of the stock markets. The ultimate goal is to spread vital knowledge and benefit the maximum audience. Her Chartered Accountant background acts as the knowledge base to help clarify crucial concepts and create a sound investment portfolio.
India is increasingly becoming a dominant options trading market with the highes...
Options trading is one of the most significant trading segments and is gaining i...
Options Greeks are an important concept in options trading and understanding the...
