Option Greek - Delta

The use of mathematical models and indicators for effective trading is not new to the markets. With the increase in technology-backed trading, there are an increasing number of traders in the derivative market trying to understand the market better and gain their footing. Option trading is a popular mode of trading in the derivative market, however, it requires a deeper understanding of all the related concepts including option greeks. In the earlier blog, we discussed the broad idea of option greeks. We will now discuss each of the option greeks in detail, starting with delta greek. Given here is the meaning and other related information on delta greeks to provide a better understanding of the concept and aid in effective trading. 

Read More: Best trading strategies for beginners

What is Delta Greek?

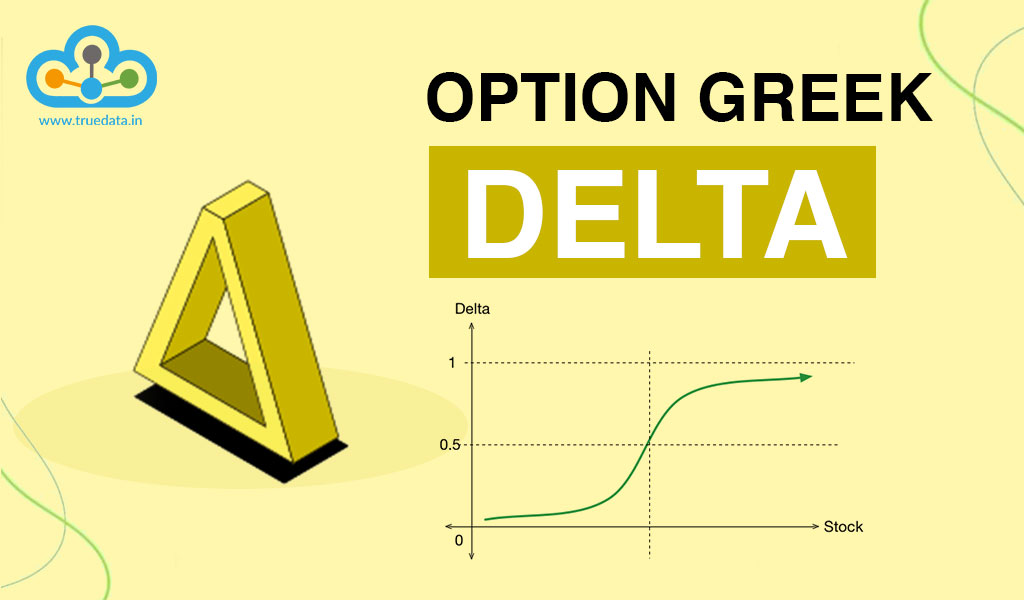
Delta is a term used in finance and trading to measure the sensitivity of an option's price to changes in the price of the underlying asset. In simple words, it tells you how much the option's price is likely to change when the price of the asset moves.

Delta is represented by a number between 0 and 1 for call options and between 0 and -1 for put options. If an option has a delta of 0.5, it means that for every Rs. 10 increase in the underlying asset's price, the option's price is expected to increase by Rs. 5. Similarly, for every Rs. 10 decrease in the asset's price, the option's price would be expected to decrease by Rs. 5.

Understanding delta is important because it helps traders assess the risk and potential profitability of their option positions. A higher delta indicates that an option's price is likely to move more in line with the underlying asset, while a lower delta suggests a smaller price change.

For example, if you are a trader in India and you buy a call option on a stock with a delta of 0.7, and the stock price goes up by Rs. 10, you can expect the option price to increase by around Rs. 7. However, if the stock price goes down by Rs. 10, the option price would likely decrease by around Rs. 7.

How to calculate Delta Greeks?

The formula to calculate Delta is as follows:

Delta = (Change in Option Price) / (Change in Price of the Underlying Asset)

In mathematical notation:

Δ = (ΔOption Price) / (ΔUnderlying Asset Price)

The numerator represents the change in the option price, which is the difference between the new option price and the original option price.

The denominator represents the change in the price of the underlying asset, which is the difference between the new price of the underlying asset and the original price.

By dividing the change in option price by the change in underlying asset price, traders can obtain the Delta value, which indicates the sensitivity of the option price to changes in the underlying asset price.

How to interpret Delta Greeks?

The concept of delta greeks is one of the primary concepts in understanding the option greeks. The interpretation of delta greeks is not limited to just understanding the relative options of the understanding asset but can collectively be also used to understand the market trend or the market sentiment. Some of the key interpretations of the delta greeks are explained below.

• Delta value

Delta represents the sensitivity of an option's price to changes in the price of the underlying asset. It ranges between 0 and 1 for call options and between 0 and -1 for put options. A Delta of 0.5 means that for every Rs.10 change in the underlying asset's price, the option's price is expected to change by Rs.5.

• Positive and negative Delta

The magnitude of Delta reflects the degree of price movement in the option relative to the underlying asset. For example, if an option has a Delta of 0.7, it suggests that the option's price is likely to change by 70% of the change in the underlying asset's price. A higher Delta indicates a stronger correlation between the option and the underlying asset, implying that the option price is expected to move more closely in line with the underlying asset's price.

• Magnitude of Delta

Delta values can vary based on the option's position relative to the current price of the underlying asset. An ITM option is one where the strike price is favorable compared to the current price of the underlying asset. ITM options typically have a Delta closer to 1 for calls (or -1 for puts), indicating a higher correlation with the underlying asset's price. ATM options have a Delta around 0.5, meaning they are less sensitive to small price changes in the underlying asset. OTM options have Deltas closer to 0, indicating a lower correlation with the underlying asset's price.

• In-the-money (ITM), at-the-money (ATM), and out-of-the-money (OTM)

Delta values can vary based on the option's position relative to the current price of the underlying asset. An ITM option is one where the strike price is favorable compared to the current price of the underlying asset. ITM options typically have a Delta closer to 1 for calls (or -1 for puts), indicating a higher correlation with the underlying asset's price. ATM options have a Delta around 0.5, meaning they are less sensitive to small price changes in the underlying asset. OTM options have Deltas closer to 0, indicating a lower correlation with the underlying asset's price.

• Delta as probability

Delta can also be interpreted as the probability of an option expiring in-the-money. For example, if an option has a Delta of 0.6, it suggests a 60% chance that the option will be profitable at expiration. While it is not a direct measure of probability, Delta can provide a rough estimate of the likelihood of an option being profitable based on its current Delta value.

• Delta and time

Delta values can change over time, especially as the option approaches its expiration date. Deltas tend to increase for ITM options and decrease for OTM options as expiration approaches. This is because ITM options have a higher probability of staying profitable, leading to higher Delta values. Conversely, OTM options become less likely to become profitable as expiration nears, resulting in lower Delta values.

• Portfolio Delta

If a trader holds multiple options or a combination of options and the underlying asset, the overall Delta of the portfolio can be calculated. Portfolio Delta helps assess the net directional exposure of the positions to changes in the underlying asset's price. A positive portfolio Delta suggests a bullish stance, as the portfolio is expected to benefit from an increase in the underlying asset's price. Conversely, a negative portfolio Delta indicates a bearish stance, as the portfolio is positioned to benefit from a decrease in the underlying asset's price.

What are the uses of Delta Greeks?

While the concept of delta greeks seems quite technical for traders, it has many wide implications or uses. Some of these uses are highlighted below.

• Managing risk

Delta helps traders manage their risk exposure. By understanding the Delta of their option positions or portfolio, traders can assess the potential profit or loss resulting from changes in the underlying asset's price. For instance, a higher Delta implies a greater potential for profit or loss. By monitoring and adjusting positions with different Deltas, traders can better control and mitigate their risk.

• Assessing price sensitivity

Delta provides valuable information about how an option's price is likely to respond to changes in the price of the underlying asset. For example, if an option has a Delta of 0.5, it means that for every Rs. 1 change in the underlying asset's price, the option's price is expected to change by approximately Rs. 0.50. This allows traders to gauge the potential impact of price movements on their option positions.

• Position adjustment

Delta helps traders make informed decisions about adjusting their option positions. As the underlying asset's price moves, the Delta of the options may change. If an option's Delta increases significantly due to a substantial gain in the underlying asset's price, a trader may consider reducing the position to lock in profits and decrease risk exposure. This adjustment helps manage risk and optimize potential returns.

• Hedging strategies

Delta can be utilized to implement hedging strategies. Hedging involves taking offsetting positions to reduce or eliminate risk. By constructing a hedge using options and the underlying asset with offsetting Delta values, traders can minimize potential losses if the market moves against their positions. Delta-neutral strategies aim to create a portfolio with a Delta value of zero, making it less sensitive to price changes.

• Probability assessment

Delta can serve as a rough estimation of the probability of an option expiring in-the-money. In simple terms, a higher Delta indicates a higher likelihood of the option being profitable at expiration. For instance, if an option has a Delta of 0.7, it suggests a 70% chance of the option expiring in a profitable state. Traders can use this probability assessment as a factor when selecting and managing their option positions.

• Portfolio management

By considering Delta Greeks collectively, traders gain insights into the overall risk and exposure of their options portfolio. Analyzing the Delta of individual positions and the portfolio as a whole helps traders assess their overall risk profile and make strategic adjustments. For instance, balancing positive and negative Deltas in the portfolio allows traders to manage directional risk and potentially enhance the portfolio's performance.

• Trading strategies

Delta can be incorporated into trading strategies to align with specific market expectations. Traders can select options with desired Delta values based on their outlook for the underlying asset. For example, if a trader anticipates a significant upward movement in a stock price, they may prefer options with higher positive Deltas to capture potential gains. Traders can, therefore, tailor their strategies by leveraging Delta to match their market views.

Conclusion

Delta greeks is the first level of greeks under options trading. Traders need to understand that there are other levels of option greeks that provide more insight or additional dimensions of analysis and risk management. A comprehensive understanding of all the Greeks helps traders make well-informed decisions and navigate the complexities of options trading effectively. Hope this blog on delta greeks was able to provide sound information on the delta greeks and a better understanding of the same. Let us know if you have any queries or need more information in this regard. Till the Happy Reading!